Control Flow

Logic, like whiskey, loses its beneficial effect when taken in too large quantities.

Edward John Moreton Drax Plunkett, Lord Dunsany

Compared to last chapter’s grueling marathon, today is a lighthearted frolic through a daisy meadow. But while the work is easy, the reward is surprisingly large.

Right now, our interpreter is little more than a calculator. A Lox program can only do a fixed amount of work before completing. To make it run twice as long you have to make the source code twice as lengthy. We’re about to fix that. In this chapter, our interpreter takes a big step towards the programming language major leagues: Turing-completeness.

9 . 1Turing Machines (Briefly)

In the early part of last century, mathematicians stumbled into a series of confusing paradoxes that led them to doubt the stability of the foundation they had built their work upon. To address that crisis, they went back to square one. Starting from a handful of axioms, logic, and set theory, they hoped to rebuild mathematics on top of an impervious foundation.

They wanted to rigorously answer questions like, “Can all true statements be proven?”, “Can we compute all functions that we can define?”, or even the more general question, “What do we mean when we claim a function is ‘computable’?”

They presumed the answer to the first two questions would be “yes”. All that remained was to prove it. It turns out that the answer to both is “no”, and astonishingly, the two questions are deeply intertwined. This is a fascinating corner of mathematics that touches fundamental questions about what brains are able to do and how the universe works. I can’t do it justice here.

What I do want to note is that in the process of proving that the answer to the first two questions is “no”, Alan Turing and Alonzo Church devised a precise answer to the last question—a definition of what kinds of functions are computable. They each crafted a tiny system with a minimum set of machinery that is still powerful enough to compute any of a (very) large class of functions.

These are now considered the “computable functions”. Turing’s system is called a Turing machine. Church’s is the lambda calculus. Both are still widely used as the basis for models of computation and, in fact, many modern functional programming languages use the lambda calculus at their core.

Turing machines have better name recognition—there’s no Hollywood film about Alonzo Church yet—but the two formalisms are equivalent in power. In fact, any programming language with some minimal level of expressiveness is powerful enough to compute any computable function.

You can prove that by writing a simulator for a Turing machine in your language. Since Turing proved his machine can compute any computable function, by extension, that means your language can too. All you need to do is translate the function into a Turing machine, and then run that on your simulator.

If your language is expressive enough to do that, it’s considered Turing-complete. Turing machines are pretty dang simple, so it doesn’t take much power to do this. You basically need arithmetic, a little control flow, and the ability to allocate and use (theoretically) arbitrary amounts of memory. We’ve got the first. By the end of this chapter, we’ll have the second.

9 . 2Conditional Execution

Enough history, let’s jazz up our language. We can divide control flow roughly into two kinds:

• Conditional or branching control flow is used to not execute some piece of code. Imperatively, you can think of it as jumping ahead over a region of code.

• Looping control flow executes a chunk of code more than once. It jumps back so that you can do something again. Since you don’t usually want infinite loops, it typically has some conditional logic to know when to stop looping as well.

Branching is simpler, so we’ll start there. C-derived languages have two main conditional execution features, the if statement and the perspicaciously named “conditional” operator (?:). An if statement lets you conditionally execute statements and the conditional operator lets you conditionally execute expressions.

For simplicity’s sake, Lox doesn’t have a conditional operator, so let’s get our if statement on. Our statement grammar gets a new production.

statement      → exprStmt
               | ifStmt
               | printStmt
               | block ;

ifStmt         → "if" "(" expression ")" statement
               ( "else" statement )? ;

An if statement has an expression for the condition, then a statement to execute if the condition is truthy. Optionally, it may also have an else keyword and a statement to execute if the condition is falsey. The syntax tree node has fields for each of those three pieces.

      "Expression : Expr expression",

      "If         : Expr condition, Stmt thenBranch," +
                  " Stmt elseBranch",

      "Print      : Expr expression",

Like other statements, the parser recognizes an if statement by the leading if keyword.

  private Stmt statement() {

    if (match(IF)) return ifStatement();

    if (match(PRINT)) return printStatement();

When it finds one, it calls this new method to parse the rest:

  private Stmt ifStatement() {
    consume(LEFT_PAREN, "Expect '(' after 'if'.");
    Expr condition = expression();
    consume(RIGHT_PAREN, "Expect ')' after if condition."); 

    Stmt thenBranch = statement();
    Stmt elseBranch = null;
    if (match(ELSE)) {
      elseBranch = statement();
    }

    return new Stmt.If(condition, thenBranch, elseBranch);
  }

As usual, the parsing code hews closely to the grammar. It detects an else clause by looking for the preceding else keyword. If there isn’t one, the elseBranch field in the syntax tree is null.

That seemingly innocuous optional else has, in fact, opened up an ambiguity in our grammar. Consider:

if (first) if (second) whenTrue(); else whenFalse();

Here’s the riddle: Which if statement does that else clause belong to? This isn’t just a theoretical question about how we notate our grammar. It actually affects how the code executes:

• If we attach the else to the first if statement, then whenFalse() is called if first is falsey, regardless of what value second has.

• If we attach it to the second if statement, then whenFalse() is only called if first is truthy and second is falsey.

Since else clauses are optional, and there is no explicit delimiter marking the end of the if statement, the grammar is ambiguous when you nest ifs in this way. This classic pitfall of syntax is called the dangling else problem.

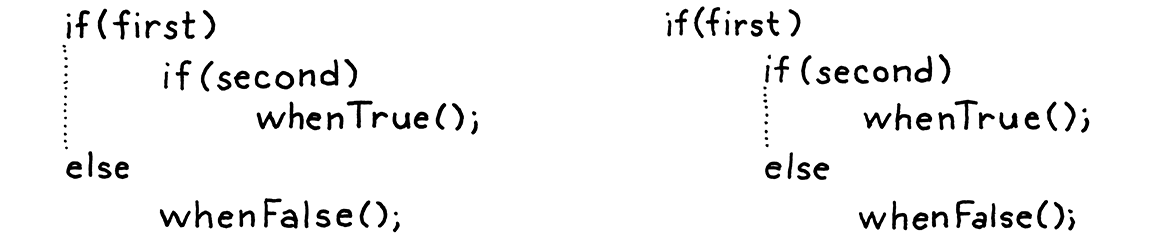
It is possible to define a context-free grammar that avoids the ambiguity directly, but it requires splitting most of the statement rules into pairs, one that allows an if with an else and one that doesn’t. It’s annoying.

Instead, most languages and parsers avoid the problem in an ad hoc way. No matter what hack they use to get themselves out of the trouble, they always choose the same interpretation—the else is bound to the nearest if that precedes it.

Our parser conveniently does that already. Since ifStatement() eagerly looks for an else before returning, the innermost call to a nested series will claim the else clause for itself before returning to the outer if statements.

Syntax in hand, we are ready to interpret.

  @Override
  public Void visitIfStmt(Stmt.If stmt) {
    if (isTruthy(evaluate(stmt.condition))) {
      execute(stmt.thenBranch);
    } else if (stmt.elseBranch != null) {
      execute(stmt.elseBranch);
    }
    return null;
  }

The interpreter implementation is a thin wrapper around the self-same Java code. It evaluates the condition. If truthy, it executes the then branch. Otherwise, if there is an else branch, it executes that.

If you compare this code to how the interpreter handles other syntax we’ve implemented, the part that makes control flow special is that Java if statement. Most other syntax trees always evaluate their subtrees. Here, we may not evaluate the then or else statement. If either of those has a side effect, the choice not to evaluate it becomes user visible.

9 . 3Logical Operators

Since we don’t have the conditional operator, you might think we’re done with branching, but no. Even without the ternary operator, there are two other operators that are technically control flow constructs—the logical operators and and or.

These aren’t like other binary operators because they short-circuit. If, after evaluating the left operand, we know what the result of the logical expression must be, we don’t evaluate the right operand. For example:

false and sideEffect();

For an and expression to evaluate to something truthy, both operands must be truthy. We can see as soon as we evaluate the left false operand that that isn’t going to be the case, so there’s no need to evaluate sideEffect() and it gets skipped.

This is why we didn’t implement the logical operators with the other binary operators. Now we’re ready. The two new operators are low in the precedence table. Similar to || and && in C, they each have their own precedence with or lower than and. We slot them right between assignment and equality.

expression     → assignment ;
assignment     → IDENTIFIER "=" assignment
               | logic_or ;
logic_or       → logic_and ( "or" logic_and )* ;
logic_and      → equality ( "and" equality )* ;

Instead of falling back to equality, assignment now cascades to logic_or. The two new rules, logic_or and logic_and, are similar to other binary operators. Then logic_and calls out to equality for its operands, and we chain back to the rest of the expression rules.

We could reuse the existing Expr.Binary class for these two new expressions since they have the same fields. But then visitBinaryExpr() would have to check to see if the operator is one of the logical operators and use a different code path to handle the short circuiting. I think it’s cleaner to define a new class for these operators so that they get their own visit method.

      "Literal  : Object value",

      "Logical  : Expr left, Token operator, Expr right",

      "Unary    : Token operator, Expr right",

To weave the new expressions into the parser, we first change the parsing code for assignment to call or().

  private Expr assignment() {

    Expr expr = or();

    if (match(EQUAL)) {

The code to parse a series of or expressions mirrors other binary operators.

  private Expr or() {
    Expr expr = and();

    while (match(OR)) {
      Token operator = previous();
      Expr right = and();
      expr = new Expr.Logical(expr, operator, right);
    }

    return expr;
  }

Its operands are the next higher level of precedence, the new and expression.

  private Expr and() {
    Expr expr = equality();

    while (match(AND)) {
      Token operator = previous();
      Expr right = equality();
      expr = new Expr.Logical(expr, operator, right);
    }

    return expr;
  }

That calls equality() for its operands, and with that, the expression parser is all tied back together again. We’re ready to interpret.

  @Override
  public Object visitLogicalExpr(Expr.Logical expr) {
    Object left = evaluate(expr.left);

    if (expr.operator.type == TokenType.OR) {
      if (isTruthy(left)) return left;
    } else {
      if (!isTruthy(left)) return left;
    }

    return evaluate(expr.right);
  }

If you compare this to the earlier chapter’s visitBinaryExpr() method, you can see the difference. Here, we evaluate the left operand first. We look at its value to see if we can short-circuit. If not, and only then, do we evaluate the right operand.

The other interesting piece here is deciding what actual value to return. Since Lox is dynamically typed, we allow operands of any type and use truthiness to determine what each operand represents. We apply similar reasoning to the result. Instead of promising to literally return true or false, a logic operator merely guarantees it will return a value with appropriate truthiness.

Fortunately, we have values with proper truthiness right at hand—the results of the operands themselves. So we use those. For example:

print "hi" or 2; // "hi".
print nil or "yes"; // "yes".

On the first line, "hi" is truthy, so the or short-circuits and returns that. On the second line, nil is falsey, so it evaluates and returns the second operand, "yes".

That covers all of the branching primitives in Lox. We’re ready to jump ahead to loops. You see what I did there? Jump. Ahead. Get it? See, it’s like a reference to . . . oh, forget it.

9 . 4While Loops

Lox features two looping control flow statements, while and for. The while loop is the simpler one, so we’ll start there. Its grammar is the same as in C.

statement      → exprStmt
               | ifStmt
               | printStmt
               | whileStmt
               | block ;

whileStmt      → "while" "(" expression ")" statement ;

We add another clause to the statement rule that points to the new rule for while. It takes a while keyword, followed by a parenthesized condition expression, then a statement for the body. That new grammar rule gets a syntax tree node.

      "Print      : Expr expression",

      "Var        : Token name, Expr initializer",

      "While      : Expr condition, Stmt body"

    ));

The node stores the condition and body. Here you can see why it’s nice to have separate base classes for expressions and statements. The field declarations make it clear that the condition is an expression and the body is a statement.

Over in the parser, we follow the same process we used for if statements. First, we add another case in statement() to detect and match the leading keyword.

    if (match(PRINT)) return printStatement();

    if (match(WHILE)) return whileStatement();

    if (match(LEFT_BRACE)) return new Stmt.Block(block());

That delegates the real work to this method:

  private Stmt whileStatement() {
    consume(LEFT_PAREN, "Expect '(' after 'while'.");
    Expr condition = expression();
    consume(RIGHT_PAREN, "Expect ')' after condition.");
    Stmt body = statement();

    return new Stmt.While(condition, body);
  }

The grammar is dead simple and this is a straight translation of it to Java. Speaking of translating straight to Java, here’s how we execute the new syntax:

  @Override
  public Void visitWhileStmt(Stmt.While stmt) {
    while (isTruthy(evaluate(stmt.condition))) {
      execute(stmt.body);
    }
    return null;
  }

Like the visit method for if, this visitor uses the corresponding Java feature. This method isn’t complex, but it makes Lox much more powerful. We can finally write a program whose running time isn’t strictly bound by the length of the source code.

9 . 5For Loops

We’re down to the last control flow construct, Ye Olde C-style for loop. I probably don’t need to remind you, but it looks like this:

for (var i = 0; i < 10; i = i + 1) print i;

In grammarese, that’s:

statement      → exprStmt
               | forStmt
               | ifStmt
               | printStmt
               | whileStmt
               | block ;

forStmt        → "for" "(" ( varDecl | exprStmt | ";" )
                 expression? ";"
                 expression? ")" statement ;

Inside the parentheses, you have three clauses separated by semicolons:

1. The first clause is the initializer. It is executed exactly once, before anything else. It’s usually an expression, but for convenience, we also allow a variable declaration. In that case, the variable is scoped to the rest of the for loop—the other two clauses and the body.

2. Next is the condition. As in a while loop, this expression controls when to exit the loop. It’s evaluated once at the beginning of each iteration, including the first. If the result is truthy, it executes the loop body. Otherwise, it bails.

3. The last clause is the increment. It’s an arbitrary expression that does some work at the end of each loop iteration. The result of the expression is discarded, so it must have a side effect to be useful. In practice, it usually increments a variable.

Any of these clauses can be omitted. Following the closing parenthesis is a statement for the body, which is typically a block.

9 . 5 . 1Desugaring

That’s a lot of machinery, but note that none of it does anything you couldn’t do with the statements we already have. If for loops didn’t support initializer clauses, you could just put the initializer expression before the for statement. Without an increment clause, you could simply put the increment expression at the end of the body yourself.

In other words, Lox doesn’t need for loops, they just make some common code patterns more pleasant to write. These kinds of features are called syntactic sugar. For example, the previous for loop could be rewritten like so:

{
  var i = 0;
  while (i < 10) {
    print i;
    i = i + 1;
  }
}

This script has the exact same semantics as the previous one, though it’s not as easy on the eyes. Syntactic sugar features like Lox’s for loop make a language more pleasant and productive to work in. But, especially in sophisticated language implementations, every language feature that requires back-end support and optimization is expensive.

We can have our cake and eat it too by desugaring. That funny word describes a process where the front end takes code using syntax sugar and translates it to a more primitive form that the back end already knows how to execute.

We’re going to desugar for loops to the while loops and other statements the interpreter already handles. In our simple interpreter, desugaring really doesn’t save us much work, but it does give me an excuse to introduce you to the technique. So, unlike the previous statements, we won’t add a new syntax tree node. Instead, we go straight to parsing. First, add an import we’ll need soon.

import java.util.ArrayList;

import java.util.Arrays;

import java.util.List;

Like every statement, we start parsing a for loop by matching its keyword.

  private Stmt statement() {

    if (match(FOR)) return forStatement();

    if (match(IF)) return ifStatement();

Here is where it gets interesting. The desugaring is going to happen here, so we’ll build this method a piece at a time, starting with the opening parenthesis before the clauses.

  private Stmt forStatement() {
    consume(LEFT_PAREN, "Expect '(' after 'for'.");

    // More here...
  }

The first clause following that is the initializer.

    consume(LEFT_PAREN, "Expect '(' after 'for'.");

    Stmt initializer;
    if (match(SEMICOLON)) {
      initializer = null;
    } else if (match(VAR)) {
      initializer = varDeclaration();
    } else {
      initializer = expressionStatement();
    }

  }

If the token following the ( is a semicolon then the initializer has been omitted. Otherwise, we check for a var keyword to see if it’s a variable declaration. If neither of those matched, it must be an expression. We parse that and wrap it in an expression statement so that the initializer is always of type Stmt.

Next up is the condition.

      initializer = expressionStatement();
    }

    Expr condition = null;
    if (!check(SEMICOLON)) {
      condition = expression();
    }
    consume(SEMICOLON, "Expect ';' after loop condition.");

  }

Again, we look for a semicolon to see if the clause has been omitted. The last clause is the increment.

    consume(SEMICOLON, "Expect ';' after loop condition.");

    Expr increment = null;
    if (!check(RIGHT_PAREN)) {
      increment = expression();
    }
    consume(RIGHT_PAREN, "Expect ')' after for clauses.");

  }

It’s similar to the condition clause except this one is terminated by the closing parenthesis. All that remains is the body.

    consume(RIGHT_PAREN, "Expect ')' after for clauses.");

    Stmt body = statement();

    return body;

  }

We’ve parsed all of the various pieces of the for loop and the resulting AST nodes are sitting in a handful of Java local variables. This is where the desugaring comes in. We take those and use them to synthesize syntax tree nodes that express the semantics of the for loop, like the hand-desugared example I showed you earlier.

The code is a little simpler if we work backward, so we start with the increment clause.

    Stmt body = statement();

    if (increment != null) {
      body = new Stmt.Block(
          Arrays.asList(
              body,
              new Stmt.Expression(increment)));
    }

    return body;

The increment, if there is one, executes after the body in each iteration of the loop. We do that by replacing the body with a little block that contains the original body followed by an expression statement that evaluates the increment.

    }

    if (condition == null) condition = new Expr.Literal(true);
    body = new Stmt.While(condition, body);

    return body;

Next, we take the condition and the body and build the loop using a primitive while loop. If the condition is omitted, we jam in true to make an infinite loop.

    body = new Stmt.While(condition, body);

    if (initializer != null) {
      body = new Stmt.Block(Arrays.asList(initializer, body));
    }

    return body;

Finally, if there is an initializer, it runs once before the entire loop. We do that by, again, replacing the whole statement with a block that runs the initializer and then executes the loop.

That’s it. Our interpreter now supports C-style for loops and we didn’t have to touch the Interpreter class at all. Since we desugared to nodes the interpreter already knows how to visit, there is no more work to do.

Finally, Lox is powerful enough to entertain us, at least for a few minutes. Here’s a tiny program to print the first 21 elements in the Fibonacci sequence:

var a = 0;
var temp;

for (var b = 1; a < 10000; b = temp + b) {
  print a;
  temp = a;
  a = b;
}