Parsing Expressions
This book is a work in progress!
×If you see a mistake, find something unclear, or have a suggestion, please let me know. To follow its progress, please join the mailing list:
(I post about once a month. Don’t worry, I won’t spam you.)
Grammar, which knows how to control even kings. Molière
This chapter marks the first major milestone of the book. Many of us have cobbled together a mishmash of regular expressions and substring operations to extract some sense out of a pile of text. The code was probably riddled with bugs and a beast to maintain. Writing a real parser—one with decent error handling, a coherent internal structure, and the ability to robustly chew through a sophisticated syntax—is considered a rare, impressive skill. In this chapter, you will attain it.
It’s easier than you think, partially because we front-loaded a lot of the hard work in the last chapter. You already know your way around a formal grammar. You’re familiar with syntax trees, and we have some Java classes to represent them. The only remaining piece is parsing—transmogrifying a sequence of tokens into one of those syntax trees.
Some CS textbooks make a big deal out of parsers. In the ’60s, computer scientists—understandably tired of programming in assembly language—started designing more sophisticated, human-friendly languages like Fortran and ALGOL. Alas, they weren’t very machine-friendly for the primitive computers of the time.
These pioneers designed languages that they honestly weren’t even sure how to write compilers for, and then did groundbreaking work inventing parsing and compiling techniques that could handle these new, big languages on those old, tiny machines.
Classic compiler books read like fawning hagiographies of these heroes and their tools. The cover of Compilers: Principles, Techniques, and Tools literally has a dragon labeled “complexity of compiler design” being slain by a knight bearing a sword and shield branded “LALR parser generator” and “syntax directed translation”. They laid it on thick.
A little self-congratulation is well-deserved, but the truth is you don’t need to know most of that stuff to bang out a high quality parser for a modern machine. As always, I encourage you to broaden your education and take it in later, but this book omits the trophy case.
6 . 1Ambiguity and the Parsing Game
In the last chapter, I said you can “play” a context-free grammar like a game in order to generate strings. Parsers play that game in reverse. Given a string—a series of tokens—we map those tokens to terminals in the grammar to figure out which rules could have generated that string.
The “could have” part is interesting. It’s entirely possible to create a grammar that is ambiguous, where different choices of productions can lead to the same string. When you’re using the grammar to generate strings, that doesn’t matter much. Once you have the string, who cares how you got to it?
When parsing, ambiguity means the parser may misunderstand the user’s code. As we parse, we aren’t just determining if the string is valid Lox code, we’re also tracking which rules match which parts of it so that we know what part of the language each token belongs to. Here’s the Lox expression grammar we put together in the last chapter:
expression → literal | unary | binary | grouping ; literal → NUMBER | STRING | "true" | "false" | "nil" ; grouping → "(" expression ")" ; unary → ( "-" | "!" ) expression ; binary → expression operator expression ; operator → "==" | "!=" | "<" | "<=" | ">" | ">=" | "+" | "-" | "*" | "/" ;
This is a valid string in that grammar:

But there are two ways we could have generated it. One way is:
- Starting at
expression, pickbinary. - For the left-hand
expression, pickNUMBER, and use6. - For the operator, pick
"/". - For the right-hand
expression, pickbinaryagain. - In that nested
binaryexpression, pick3 - 1.
Another is:
- Starting at
expression, pickbinary. - For the left-hand
expression, pickbinaryagain. - In that nested
binaryexpression, pick6 / 3. - Back at the outer
binary, for the operator, pick"-". - For the right-hand
expression, pickNUMBER, and use1.
Those produce the same strings, but not the same syntax trees:
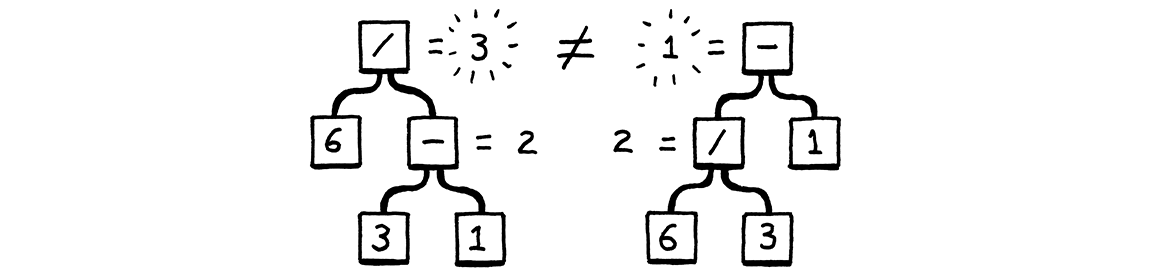
In other words, the grammar allows seeing the expression as (6 / 3) - 1 or 6 / (3 - 1). The binary rule lets operands nest any which way you want. That in
turn affects the result of evaluating the parsed tree. The way mathematicians
have addressed this ambiguity since blackboards were first invented is by
defining rules for precedence and associativity.
-
Precedence determines which operator is evaluated first in an expression containing a mixture of different operators. Precedence rules tell us that we evaluate the
/before the-in the above example. Operators with higher precedence are evaluated before operators with lower precedence. Equivalently, higher precedence operators are said to “bind tighter”. -
Associativity determines which operator is evaluated first in a series of the same operator. When an operator is left-associative (think “left-to-right”), operators on the left evaluate before those on the right. Since
-is left-associative, this expression:5 - 3 - 1
is equivalent to:
(5 - 3) - 1
Assignment, on the other hand, is right-associative. This:
a = b = c
is equivalent to:
a = (b = c)
Without well-defined precedence and associativity, an expression that uses multiple operators is ambiguous—it can be parsed into different syntax trees, which could in turn evaluate to different results. We’ll fix that in Lox by applying the same precedence rules as C, going from lowest to highest.
| Name | Operators | Associates |
| Equality | == != |
Left |
| Comparison | > >=
< <= |
Left |
| Term | - + |
Left |
| Factor | / * |
Left |
| Unary | ! - |
Right |
Right now, the grammar stuffs all expression types into a single expression
rule. That same rule is used as the non-terminal for operands, which lets the
grammar accept any kind of expression as a subexpression, regardless of whether
the precedence rules allow it.
We fix that by stratifying the grammar. We define a separate rule for each precedence level.
expression → ... equality → ... comparison → ... term → ... factor → ... unary → ... primary → ...
Each rule here only matches expressions at its precedence level or higher. For
example, unary matches a unary expression like !negated or a primary
expression like 1234. And term can match 1 + 2 but also 3 * 4 / 5. The
final primary rule covers the highest-precedence forms—literals and
parenthesized expressions.
We just need to fill in the productions for each of those rules. We’ll do the
easy ones first. The top expression rule matches any expression at any
precedence level. Since equality has the lowest
precedence, if we match that, then it covers everything.
expression → equality
Over at the other end of the precedence table, a primary expression contains all the literals and grouping expressions.
primary → NUMBER | STRING | "true" | "false" | "nil" | "(" expression ")" ;
A unary expression starts with a unary operator followed by the operand. Since
unary operators can nest—!!true is a valid if weird expression—the
operand can itself be a unary operator. A recursive rule handles that nicely.
unary → ( "!" | "-" ) unary ;
But this rule has a problem. It never terminates.
Remember, each rule needs to match expressions at that precedence level or higher, so we also need to let this match a primary expression.
unary → ( "!" | "-" ) unary | primary ;
That works.
The remaining rules are all binary operators. We’ll start with the rule for multiplication and division. Here’s a first try:
factor → factor ( "/" | "*" ) unary | unary ;
The rule recurses to match the left operand. That enables the rule to match a
series of multiplication and division expressions like 1 * 2 / 3. Putting the
recursive production on the left side and unary on the right makes the rule
left-associative and unambiguous.
All of this is correct, but the fact that the first symbol in the body of the
rule is the same as the head of the rule means this production is
left-recursive. Some parsing techniques, including the one we’re going to
use, have trouble with left recursion. (Recursion elsewhere, like we have in
unary and the indirect recursion for grouping in primary are not a problem.)
There are many grammars you can define that match the same language. The choice for how to model a particular language is partially a matter of taste and partially a pragmatic one. This rule is correct, but not optimal for how we intend to parse it. Instead of a left recursive rule, we’ll use a different one.
factor → unary ( ( "/" | "*" ) unary )* ;
We define a factor expression as a flat sequence of multiplications and divisions. This matches the same syntax as the previous rule, but better mirrors the code we’ll write to parse Lox. We use the same structure for all of the other binary operator precedence levels, giving us this complete expression grammar:
expression → equality ; equality → comparison ( ( "!=" | "==" ) comparison )* ; comparison → term ( ( ">" | ">=" | "<" | "<=" ) term )* ; term → factor ( ( "-" | "+" ) factor )* ; factor → unary ( ( "/" | "*" ) unary )* ; unary → ( "!" | "-" ) unary | primary ; primary → NUMBER | STRING | "true" | "false" | "nil" | "(" expression ")" ;
This grammar is more complex than the one we had before, but in return we have eliminated the previous one’s ambiguity. It’s just what we need to make a parser.
6 . 2Recursive Descent Parsing
There is a whole pack of parsing techniques whose names are mostly combinations of “L” and “R”—LL(k), LR(1), LALR—along with more exotic beasts like parser combinators, Earley parsers, the shunting yard algorithm, and packrat parsing. For our first interpreter, one technique is more than sufficient: recursive descent.
Recursive descent is the simplest way to build a parser, and doesn’t require using complex parser generator tools like Yacc, Bison or ANTLR. All you need is straightforward handwritten code. Don’t be fooled by its simplicity, though. Recursive descent parsers are fast, robust, and can support sophisticated error handling. In fact, GCC, V8 (the JavaScript VM in Chrome), Roslyn (the C# compiler written in C#) and many other heavyweight production language implementations use recursive descent. It rocks.
Recursive descent is considered a top-down parser because it starts from the
top or outermost grammar rule (here expression) and works its way down into the nested subexpressions before finally
reaching the leaves of the syntax tree. This is in contrast with bottom-up
parsers like LR that start with primary expressions and compose them into larger
and larger chunks of syntax.
A recursive descent parser is a literal translation of the grammar’s rules straight into imperative code. Each rule becomes a function. The body of the rule translates to code roughly like:
| Grammar notation | Code representation |
| Terminal | Code to match and consume a token |
| Nonterminal | Call to that rule’s function |
| | if or switch statement |
* or + | while or for loop |
? | if statement |
The descent is described as “recursive” because when a grammar rule refers to itself—directly or indirectly—that translates to a recursive function call.
6 . 2 . 1The parser class
Each grammar rule becomes a method inside this new class:
create new file
package com.craftinginterpreters.lox; import java.util.List; import static com.craftinginterpreters.lox.TokenType.*; class Parser { private final List<Token> tokens; private int current = 0; Parser(List<Token> tokens) { this.tokens = tokens; } }
Like the scanner, the parser consumes a flat input sequence, only now we’re
reading tokens instead of characters. We store the list of tokens and use
current to point to the next token eagerly waiting to be parsed.
We’re going to run straight through the expression grammar now and translate
each rule to Java code. The first rule, expression, simply expands to the
equality rule, so that’s straightforward.
add after Parser()
private Expr expression() { return equality(); }
Each method for parsing a grammar rule produces a syntax tree for that rule and returns it to the caller. When the body of the rule contains a nonterminal—a reference to another rule—we call that other rule’s method.
The rule for equality is a little more complex.
equality → comparison ( ( "!=" | "==" ) comparison )* ;
In Java, that becomes:
add after expression()
private Expr equality() { Expr expr = comparison(); while (match(BANG_EQUAL, EQUAL_EQUAL)) { Token operator = previous(); Expr right = comparison(); expr = new Expr.Binary(expr, operator, right); } return expr; }
Let’s step through it. The first comparison nonterminal in the body translates
to the first call to comparison() in the method. We take that result and store
it in a local variable.
Then, the ( ... )* loop in the rule maps to a while loop. We need to know
when to exit that loop. We can see that inside the rule, we must first find
either a != or == token. So, if we don’t see one of those, we must be done
with the sequence of equality operators. We express that check using a handy
match() method.
add after equality()
private boolean match(TokenType... types) { for (TokenType type : types) { if (check(type)) { advance(); return true; } } return false; }
This checks to see if the current token has any of the given types. If so, it
consumes the token and returns true. Otherwise, it returns false and leaves
the current token alone. The match() method is defined in terms of two more
fundamental operations.
The check() method returns true if the current token is of the given type.
Unlike match(), it never consumes the token, it only looks at it.
add after match()
private boolean check(TokenType type) { if (isAtEnd()) return false; return peek().type == type; }
The advance() method consumes the current token and returns it, similar to how
our scanner’s corresponding method crawled through characters.
add after check()
private Token advance() { if (!isAtEnd()) current++; return previous(); }
These methods bottom out on the last handful of primitive operations.
add after advance()
private boolean isAtEnd() { return peek().type == EOF; } private Token peek() { return tokens.get(current); } private Token previous() { return tokens.get(current - 1); }
isAtEnd() checks if we’ve run out of tokens to parse. peek() returns the
current token we have yet to consume, and previous() returns the most recently
consumed token. The latter makes it easier to use match() and then access the
just-matched token.
That’s most of the parsing infrastructure we need. Where were we? Right, so if
we are inside the while loop in equality(), then we know we have found a
!= or == operator and must be parsing an equality expression.
We grab the matched operator token so we can track which kind of equality
expression we have. Then we call comparison() again to parse the right-hand
operand. We combine the operator and its two operands into a new Expr.Binary
syntax tree node, and then loop around. For each iteration, we store the
resulting expression back in the same expr local variable. As we zip through a
sequence of equality expressions, that creates a left-associative nested tree of
binary operator nodes.
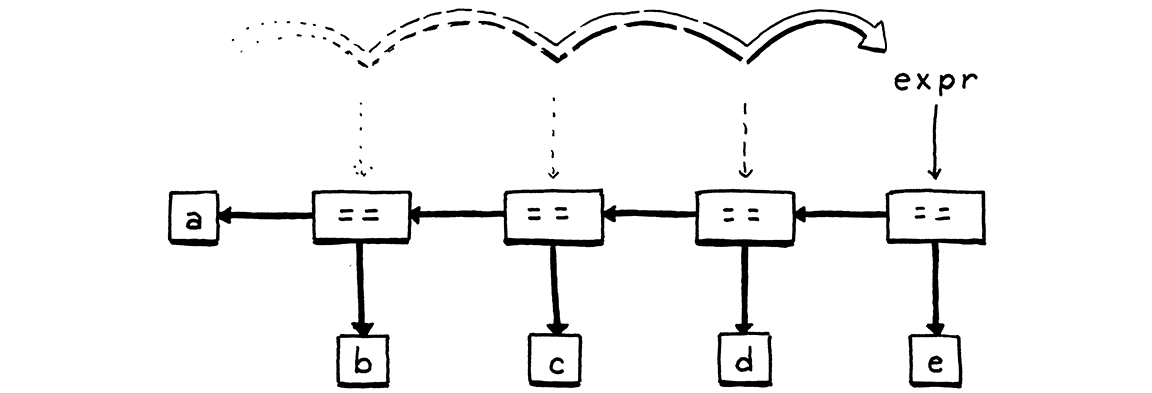
The parser falls out of the loop once it hits a token that’s not an equality
operator. Finally, it returns the expression. Note that if the parser never
encounters an equality operator, then it never enters the loop. In that case,
the equality() method effectively calls and returns comparison(). In that
way, this method matches an equality operator or anything of higher
precedence.
Moving on to the next rule . . .
comparison → term ( ( ">" | ">=" | "<" | "<=" ) term )* ;
Translated to Java:
add after equality()
private Expr comparison() { Expr expr = term(); while (match(GREATER, GREATER_EQUAL, LESS, LESS_EQUAL)) { Token operator = previous(); Expr right = term(); expr = new Expr.Binary(expr, operator, right); } return expr; }
The grammar rule is virtually identical to equality
and so is the corresponding code. The only differences are the token types for
the operators we match, and the method we call for the operands—now
term() instead of comparison(). The remaining two binary operator rules
follow the same pattern.
In order of precedence, first addition and subtraction:
add after comparison()
private Expr term() { Expr expr = factor(); while (match(MINUS, PLUS)) { Token operator = previous(); Expr right = factor(); expr = new Expr.Binary(expr, operator, right); } return expr; }
And finally, multiplication and division:
add after term()
private Expr factor() { Expr expr = unary(); while (match(SLASH, STAR)) { Token operator = previous(); Expr right = unary(); expr = new Expr.Binary(expr, operator, right); } return expr; }
That’s all of the binary operators, parsed with the correct precedence and associativity. We’re crawling up the precedence hierarchy and now we’ve reached the unary operators.
unary → ( "!" | "-" ) unary | primary ;
The code for this is a little different.
add after factor()
private Expr unary() { if (match(BANG, MINUS)) { Token operator = previous(); Expr right = unary(); return new Expr.Unary(operator, right); } return primary(); }
Again, we look at the current token to see how to
parse. If it’s a ! or -, we must have a unary expression. In that case, we
grab the token and then recursively call unary() again to parse the operand.
Wrap that all up in a unary expression syntax tree and we’re done.
Otherwise, we must have reached the highest level of precedence, primary expressions.
primary → NUMBER | STRING | "true" | "false" | "nil" | "(" expression ")" ;
Most of the cases for the rule are single terminals, so parsing is straightforward.
add after unary()
private Expr primary() { if (match(FALSE)) return new Expr.Literal(false); if (match(TRUE)) return new Expr.Literal(true); if (match(NIL)) return new Expr.Literal(null); if (match(NUMBER, STRING)) { return new Expr.Literal(previous().literal); } if (match(LEFT_PAREN)) { Expr expr = expression(); consume(RIGHT_PAREN, "Expect ')' after expression."); return new Expr.Grouping(expr); } }
The interesting branch is the one for handling parentheses. After we match an
opening ( and parse the expression inside it, we must find a ) token. If
we don’t, that’s an error.
6 . 3Syntax Errors
A parser really has two jobs:
-
Given a valid sequence of tokens, produce a corresponding syntax tree.
-
Given an invalid sequence of tokens, detect any errors and tell the user about their mistakes.
Don’t underestimate how important the second job is! In modern IDEs and editors, the parser is constantly reparsing code—often while the user is still editing it—in order to syntax highlight and support things like auto-complete. That means it will encounter code in incomplete, half-wrong states all the time.
When the user doesn’t realize the syntax is wrong, it is up to the parser to help guide them back onto the right path. The way it reports errors is a large part of your language’s user interface. Good syntax error handling is hard. By definition, the code isn’t in a well-defined state, so there’s no infallible way to know what the user meant to write. The parser can’t read your mind.
There are a couple of hard requirements for when the parser runs into a syntax error. A parser must:
-
Detect and report the error. If it doesn’t detect the error and passes the resulting malformed syntax tree on to the interpreter, all manner of horrors may be summoned.
-
Avoid crashing or hanging. Syntax errors are a fact of life, and language tools have to be robust in the face of them. Segfaulting or getting stuck in an infinite loop isn’t allowed. While the source may not be valid code, it’s still a valid input to the parser because users use the parser to learn what syntax is allowed.
Those are the table stakes if you want to get in the parser game at all, but you really want to raise the ante beyond that. A decent parser should:
-
Be fast. Computers are thousands of times faster than they were when parser technology was first invented. The days of needing to optimize your parser so that it could get through an entire source file during a coffee break are over. But programmer expectations have risen as quickly, if not faster. They expect their editors to reparse files in milliseconds after every keystroke.
-
Report as many distinct errors as there are. Aborting after the first error is easy to implement, but it’s annoying for users if every time they fix what they think is the one error in a file, a new one appears. They want to see them all.
-
Minimize cascaded errors. Once a single error is found, the parser no longer really knows what’s going on. It tries to get itself back on track and keep going, but if it gets confused, it may report a slew of ghost errors that don’t indicate other real problems in the code. When the first error is fixed, those phantoms disappear, because they reflect only the parser’s own confusion. Cascaded errors are annoying because they can scare the user into thinking their code is in a worse state than it is.
The last two points are in tension. We want to report as many separate errors as we can, but we don’t want to report ones that are merely side effects of an earlier one.
The way a parser responds to an error and keeps going to look for later errors is called error recovery. This was a hot research topic in the ’60s. Back then, you’d hand a stack of punch cards to the secretary and come back the next day to see if the compiler succeeded. With an iteration loop that slow, you really wanted to find every single error in your code in one pass.
Today, when parsers complete before you’ve even finished typing, it’s less of an issue. Simple, fast error recovery is fine.
6 . 3 . 1Panic mode error recovery
Of all the recovery techniques devised in yesteryear, the one that best stood the test of time is called—somewhat alarmingly—panic mode. As soon as the parser detects an error, it enters panic mode. It knows at least one token doesn’t make sense given its current state in the middle of some stack of grammar productions.
Before it can get back to parsing, it needs to get its state and the sequence of forthcoming tokens aligned such that the next token does match the rule being parsed. This process is called synchronization.
To do that, we select some rule in the grammar that will mark the synchronization point. The parser fixes its parsing state by jumping out of any nested productions until it gets back to that rule. Then it synchronizes the token stream by discarding tokens until it reaches one that can appear at that point in the rule.
Any additional real syntax errors hiding in those discarded tokens aren’t reported, but it also means that any mistaken cascaded errors that are side effects of the initial error aren’t falsely reported either, which is a decent trade-off.
The traditional place in the grammar to synchronize is between statements. We don’t have those yet, so we won’t actually synchronize in this chapter, but we’ll get the machinery in place for later.
6 . 3 . 2Entering panic mode
Back before we went on this side trip around error recovery, we were writing the
code to parse a parenthesized expression. After parsing the expression, it
looks for the closing ) by calling consume(). Here, finally, is that method:
add after match()
private Token consume(TokenType type, String message) { if (check(type)) return advance(); throw error(peek(), message); }
It’s similar to match() in that it checks to see if the next token is of the
expected type. If so, it consumes it and everything is groovy. If some other
token is there, then we’ve hit an error. We report it by calling this:
add after previous()
private ParseError error(Token token, String message) { Lox.error(token, message); return new ParseError(); }
First, that shows the error to the user by calling:
add after report()
static void error(Token token, String message) { if (token.type == TokenType.EOF) { report(token.line, " at end", message); } else { report(token.line, " at '" + token.lexeme + "'", message); } }
This reports an error at a given token. It shows the token’s location and the token itself. This will come in handy later since we use tokens throughout the interpreter to track locations in code.
After we report the error, the user knows about their mistake, but what does the
parser do next? Back in error(), we create and return a ParseError, an
instance of this new class:
class Parser {
nest inside class Parser
private static class ParseError extends RuntimeException {}
private final List<Token> tokens;
This is a simple sentinel class we use to unwind the parser. The error()
method returns the error instead of throwing it because we want to let the
calling method inside the parser decide whether to unwind or not. Some parse
errors occur in places where the parser isn’t likely to get into a weird state
and we don’t need to synchronize. In those
places, we simply report the error and keep on truckin’.
For example, Lox limits the number of arguments you can pass to a function. If you pass too many, the parser needs to report that error, but it can and should simply keep on parsing the extra arguments instead of freaking out and going into panic mode.
In our case, though, the syntax error is nasty enough that we want to panic and synchronize. Discarding tokens is pretty easy, but how do we synchronize the parser’s own state?
6 . 3 . 3Synchronizing a recursive descent parser
With recursive descent, the parser’s state—which rules it is in the middle of recognizing—is not stored explicitly in fields. Instead, we use Java’s own call stack to track what the parser is doing. Each rule in the middle of being parsed is a call frame on the stack. In order to reset that state, we need to clear out those call frames.
The natural way to do that in Java is exceptions. When we want to synchronize, we throw that ParseError object. Higher up in the method for the grammar rule we are synchronizing to, we’ll catch it. Since we synchronize on statement boundaries, we’ll catch the exception there. After the exception is caught, the parser is in the right state. All that’s left is to synchronize the tokens.
We want to discard tokens until we’re right at the beginning of the next
statement. That boundary is pretty easy to spot—it’s one of the main reasons
we picked it. After a semicolon, we’re probably
finished with a statement. Most statements start with a keyword—for, if,
return, var, etc. When the next token is any of those, we’re probably
about to start a statement.
This method encapsulates that logic:
add after error()
private void synchronize() { advance(); while (!isAtEnd()) { if (previous().type == SEMICOLON) return; switch (peek().type) { case CLASS: case FUN: case VAR: case FOR: case IF: case WHILE: case PRINT: case RETURN: return; } advance(); } }
It discards tokens until it thinks it has found a statement boundary. After catching a ParseError, we’ll call this and then we are hopefully back in sync. When it works well, we have discarded tokens that would have likely caused cascaded errors anyway, and now we can parse the rest of the file starting at the next statement.
Alas, we don’t get to see this method in action, since we don’t have statements yet. We’ll get to that in a couple of chapters. For now, if an error occurs, we’ll panic and unwind all the way to the top and stop parsing. Since we can parse only a single expression anyway, that’s no big loss.
6 . 4Wiring up the Parser
We are mostly done parsing expressions now. There is one other place where we
need to add a little error handling. As the parser descends through the parsing
methods for each grammar rule, it eventually hits primary(). If none of the
cases in there match, it means we are sitting on a token that can’t start an
expression. We need to handle that error too.
if (match(LEFT_PAREN)) {
Expr expr = expression();
consume(RIGHT_PAREN, "Expect ')' after expression.");
return new Expr.Grouping(expr);
}
in primary()
throw error(peek(), "Expect expression.");
}
With that, all that remains in the parser is to define an initial method to kick
it off. That method is called, naturally enough, parse().
add after Parser()
Expr parse() { try { return expression(); } catch (ParseError error) { return null; } }
We’ll revisit this method later when we add statements to the language. For now, it parses a single expression and returns it. We also have some temporary code to exit out of panic mode. Syntax error recovery is the parser’s job, so we don’t want the ParseError exception to escape into the rest of the interpreter.
When a syntax error does occur, this method returns null. That’s OK. The
parser promises not to crash or hang on invalid syntax, but it doesn’t promise
to return a usable syntax tree if an error is found. As soon as the parser
reports an error, hadError gets set, and subsequent phases are skipped.
Finally, we can hook up our brand new parser to the main Lox class and try it out. We still don’t have an interpreter, so for now, we’ll parse to a syntax tree and then use the AstPrinter class from the last chapter to display it.
Delete the old code to print the scanned tokens and replace it with this:
List<Token> tokens = scanner.scanTokens();
in run()
replace 5 lines
Parser parser = new Parser(tokens);
Expr expression = parser.parse();
// Stop if there was a syntax error.
if (hadError) return;
System.out.println(new AstPrinter().print(expression));
}
Congratulations, you have crossed the threshold! That really is all there is to handwriting a parser. We’ll extend the grammar in later chapters with assignment, statements, and other stuff, but none of that is any more complex than the binary operators we tackled here.
Fire up the interpreter and type in some expressions. See how it handles precedence and associativity correctly? Not bad for less than 200 lines of code.
Challenges
-
In C, a block is a statement form that allows you to pack a series of statements where a single one is expected. The comma operator is an analogous syntax for expressions. A comma-separated series of expressions can be given where a single expression is expected (except inside a function call’s argument list). At runtime, the comma operator evaluates the left operand and discards the result. Then it evaluates and returns the right operand.
Add support for comma expressions. Give them the same precedence and associativity as in C. Write the grammar, and then implement the necessary parsing code.
-
Likewise, add support for the C-style conditional or “ternary” operator
?:. What precedence level is allowed between the?and:? Is the whole operator left-associative or right-associative? -
Add error productions to handle each binary operator appearing without a left-hand operand. In other words, detect a binary operator appearing at the beginning of an expression. Report that as an error, but also parse and discard a right-hand operand with the appropriate precedence.
Design Note: Logic Versus History
Let’s say we decide to add bitwise & and | operators to Lox. Where should we
put them in the precedence hierarchy? C—and most languages that follow in C’s
footsteps—place them below ==. This is widely considered a mistake because
it means common operations like testing a flag require parentheses.
if (flags & FLAG_MASK == SOME_FLAG) { ... } // Wrong. if ((flags & FLAG_MASK) == SOME_FLAG) { ... } // Right.
Should we fix this for Lox and put bitwise operators higher up the precedence table than C does? There are two strategies we can take.
You almost never want to use the result of an == expression as the operand to
a bitwise operator. By making bitwise bind tighter, users don’t need to
parenthesize as often. So if we do that, and users assume the precedence is
chosen logically to minimize parentheses, they’re likely to infer it correctly.
This kind of internal consistency makes the language easier to learn because there are fewer edge cases and exceptions users have to stumble into and then correct. That’s good, because before users can use our language, they have to load all of that syntax and semantics into their heads. A simpler, more rational language makes sense.
But, for many users there is an even faster shortcut to getting our language’s ideas into their wetware—use concepts they already know. Many newcomers to our language will be coming from some other language or languages. If our language uses some of the same syntax or semantics as those, there is much less for the user to learn (and unlearn).
This is particularly helpful with syntax. You may not remember it well today, but way back when you learned your very first programming language, code probably looked alien and unapproachable. Only through painstaking effort did you learn to read and accept it. If you design a novel syntax for your new language, you force users to start that process all over again.
Taking advantage of what users already know is one of the most powerful tools you can use to ease adoption of your language. It’s almost impossible to overestimate how valuable this is. But it faces you with a nasty problem: What happens when the thing the users all know kind of sucks? C’s bitwise operator precedence is a mistake that doesn’t make sense. But it’s a familiar mistake that millions have already gotten used to and learned to live with.
Do you stay true to your language’s own internal logic and ignore history? Do you start from a blank slate and first principles? Or do you weave your language into the rich tapestry of programming history and give your users a leg up by starting from something they already know?
There is no perfect answer here, only trade-offs. You and I are obviously biased towards liking novel languages, so our natural inclination is to burn the history books and start our own story.
In practice, it’s often better to make the most of what users already know. Getting them to come to your language requires a big leap. The smaller you can make that chasm, the more people will be willing to cross it. But you can’t always stick to history, or your language won’t have anything new and compelling to give people a reason to jump over.